האם בדיקות הקורונה שגויות?

הקדמה

במאמר איך לקרוא מחקר (ג) הבאתי דוגמה של חישוב הסתברות גילוי השווא (False Detection Rate – FDR) של מחלה כלשהי. הפעם אני מחשב ערך זה עבור הבדיקות לגילוי וירוס הקורונה SARS-CoV-2.

שיטת הבדיקה

הבדיקה למציאת נגיף הקורונה נקראת RT-PCR. קיימות גרסאות שונות של בדיקה זו בתלות בחומר התגובה (reagent) שבו משתמשים.

עשיתי חיפוש נרחב של ערכי sensitivity ו-specificity של בדיקה זו, ומצאתי את הנתונים הבאים:

• קיים פיזור רב בערכי ה-sensitivity כדלהלן: sensitivity = 60% – 98%, מקור [1].
• מצאתי מעט מאד נתונים על ערכי ה-specificity. הערך הגבוה ביותר שמצאתי הוא specificity = 91%. מקור [2].

שכיחות המחלה

אוכלוסית ישראל מונה כ-9.1 מיליון תושבים. מספר הנדבקים הכולל (נכון לתאריך 16 בספטמבר) הוא 167,000. לפיכך שכיחות המחלה באוכלוסיה היא:

Prevalence(population) = 167000/9100000 ≅ 1.8%

אחוז הנדבקים לאחרונה הוא 10%, כלומר:

Prevalence(tested) = 10%

חישוב False Detection Rate

החישוב מבוסס על משפט בייס (Bayes' theorem) הדורש ידיעה מקדימה (priory) של ההסתברות הארוע הנבחן – במקרה שלנו שכיחות המחלה (prevalence).

כדי לחשב את הסתברות גילויי השווא של הבדיקה נדרשים שלושה נתונים:

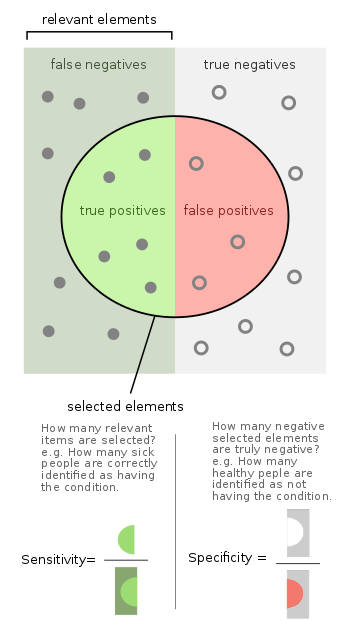
• specificity – אחוז התוצאות השליליות המאובחנות נכון
• sensitivity – אחוז התוצאות החיוביות המאובחנות נכון
• prevalence – שכיחות המחלה

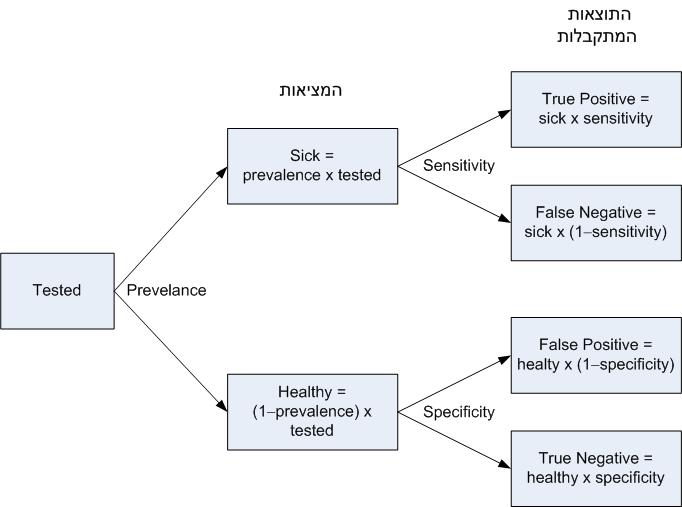
כדי לחשב איזה חלק של התוצאות החיוביות הן שגויות, עלינו להתחשב לא רק במיקרים של false positive (הענף התחתון של הציור), אלא גם במקרים של true positive (הענף העליון של הציור). לכן, המספר הכולל של תוצאות חיוביות הוא

Total positive = false positive + true positive

והסתברות לגילוי שווא היא

False Discovery Rate = false positive / (false positive + true positive)

את ערכי FDR עבור ערכים שונים של sensitivity ו-specificity, בתלות ב-prevalence חישבתי באמצעות פונקציית Matlab קטנה, והנה התוצאות.

מקרה א'

כאמור לעיל, הערך המירבי של specificity אשר מצאתי הוא 91%.

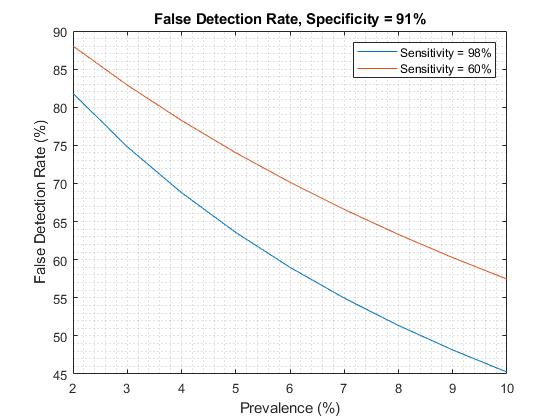
ניתן לראות כי עבור הערך הגבוה של sensitivity = 98% ושכיחות של 10% מקבלים FDR = 45%. זהו ערך בלתי נסבל, ואם נכון, מכניס כל יום קרוב ל-20,000 איש לבידוד מיותר.

מקרה ב'

נשאר לקוות כי ה-specificity גבוה יותר ממה שאני מצאתי בחיפושי. עבור specificity = 95% מקבלים

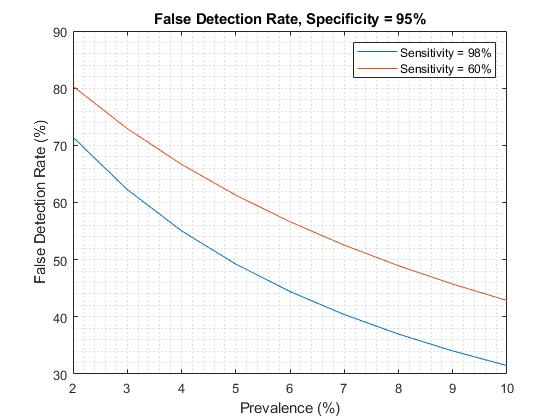
יותר טוב, אבל עדיין גרוע מאד.

מקרה ג'

עבור specificity = 98% (ואני מטיל ספק שזה אפשרי) מקבלים

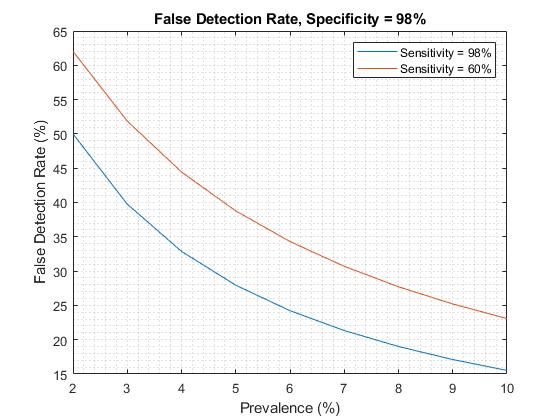
סיכום

בצירוף האופטימי ביותר:

sensitivity = 96%, specificity = 98%, prevalence = 10%

מקבלים FDR = 15%. המשמעות היא כי כל יום מוכנסים 6,000 איש לבידוד מיותר. ערכים נמוכים של אחד או יותר מהפרמטרים לעיל מגדילים את ה-FDR.

אם הנתונים שלי נכונים, אזי מסתמנת בעיה קשה של אלפי אנשים המאובחנים כנשאים של הוירוס, למרות שאין הם כאלה. המשמעות הכלכלית היא מרחיקת לכת – אלפי אנשים מוכנסים לבידוד ללא הצדקה, וחמור יותר – עלולות להתקבל החלטות בריאות ציבור מוטעות.