חלק שלישי: הפרשנות השגויה של p-value

הקדמה

במאמר איך לקרוא מחקר (ב) ראינו כי ערכו של p-value משמש כקריטריון לדחיה או קבלה של השערת האפס. אכן, p-value עושה בדיוק מה שהוא מתיימר לעשות. אם הוא קטן מספיק, הרי שלא סביר כי השערת האפס נכונה. הבעיה היא ש-p-value איננו עונה על השאלה שכל חוקר צריך לשאול את עצמו: "אם אני טוען, על בסיס תוצאות הניסוי שעשיתי, כי מצאתי תופעה בה אני מעוניין, מה ההסתברות שאני שוגה?".

התשובה המקובלת על רוב החוקרים היא כי הסתברות השגיאה היא רמת המובהקות (α) שנבחרה לניסוי. אם מתקיים p-value ≤ α הרי שהצליח להפריך את השערת האפס, והשיג את התופעה המבוקשת.

במאמר זה נבחן את אמיתות טענה זו.

אינדוקציה מול דדוקציה

השאלה איתה מתמודד חוקר היא מה ההסתברות שהוא טועה כאשר הוא טוען שתוצאה היא אמיתית, בעוד שלמעשה היא מיקרית. הוא מנסה להכליל מניסוי בודד אל הכלל:
ניסוי ← תרופה ← שימוש באוכלוסיה הכללית. זוהי שאלה באינדוקציה, וההתמודדות איתה קשה.

לעומתה, תהליך דדוקטיבי (מן הכלל אל הפרט) פשוט הרבה יותר. בהנחה שהשערה מסוימת היא נכונה, החוקר מקיש ממנה את התוצאות הצפויות, ואז משווה אותן למציאות. אם יש התאמה, ההשערה אוששה, אם אין, ההשערה הופרכה.

כדי לפתור את הבעיה, הסטטיסטיקאי רולנד פישר (Roland Fisher) הציג בשנות העשרים של המאה הקודמת שיטה של שימוש במבחנים של משמעות סטטיסטית. אלה הם מבחנים דדוקטיביים ולכן עוקפים את בעיית האינדוקציה – p-value נולד. כל מה שנשאר לעשות הוא להחליט מהו הערך הדרוש של p-value כדי להצהיר כי גילינו משהו. אבל מסתבר כי זו בעיה קשה מאד.

תשובה נכונה לשאלה לא נכונה

הבעיה היא כי p-value נותן תשובה נכונה לשאלה לא נכונה. מה שאנחנו מעוניינים לדעת איננה ההסתברות של התבוננות (A) בהנתן השערה בדבר קיומה של תוצאה אמיתית (B) (כלומר (P(A|B), אלא ההסתברות שההשערה נכונה (B), בהנתן ההתבוננות (A) (כלומר (P(B|A). הבילבול בין שתי הסתברויות אלה ניצב בליבה של הבעיה מדוע ערכי p-value מפורשים בצורה לא נכונה בכל כך הרבה מיקרים.

משפט בייס (Bayes' theorem)

הכומר תומס בייס (Thomas Bayes) פתר, בעיקרון, את הבעיה. הוא הראה איך להפוך את הסתברות להתבוננות בהנתן השערה (דדוקציה), להסתברות כי ההשערה נכונה בהנתן התבוננות (אינדוקציה). ברישום המתאים לביו-רפואה, משפט בייס אומר:

P[D|S] = k x P[S|D] x P[D]

S – סימפטום

D – מחלה

 ההסתברות למחלה בהנתן סימפטום – P[D|S]

  ההסתברות לסימפטום בהנתן מחלה – P[S|D]

לקיום המחלה (prior probability) ההסתברות המקדימה – P[D]

משפט בייס מחייב הקצאה של ההסתברות המקדימה של ההשערה לפני בצוע ההתבוננות, ומייד מתעוררת השאלה מהי ערכה של ההסתברות המקדימה לתופעה שאנו מחפשים?

בעיית בדיקות הסריקה

בדיקות סריקה (screening), להבדיל מבדיקות אבחון (diagnosis), הן בדיקות המבוצעות לאנשים בריאים כדי לגלות סימנים מוקדמים של מחלה, בטרם התגלו אצלם תסמינים כלשהם.

בבבדיקות סריקה, שכיחות המחלה באוכלוסיה (prevalence) היא ההסתברות המקדימה הדרושה לצורך שימוש במשפט בייס.

דוגמה

נבחן מהי הסתברות גילויי השווא (false discovery rate) בבדיקת סריקה לגילוי מחלה כלשהי. כדי לחשב את קצב גילויי השווא של בדיקת הסריקה נדרשים שלושה נתונים:

• specificity – אחוז התוצאות השליליות המאובחנות נכון
• sensitivity – אחוז התוצאות החיוביות המאובחנות נכון
• prevalence – שכיחות המחלה הנבדקת באוכלוסיה

נניח כי 95%  (specificity = 0.95) של הנבדקים בבדיקת הסריקה אינם סובלים מהמחלה, ומאובחנים נכון שאכן אינם סובלים ממחלה זו. 5% הנותרים הם שגיאה מסוג 1 (false positive), כלומר, אנשים שאינם סובלים מהמחלה, אך אובחנו באופן שגוי כחולים. כמו כן נניח כי 80% מהסובלים מהמחלה מתגלים בבדיקה (sensitivity = 0.8). זוהי העוצמה (power) של הבדיקה, הנקבעת על ידי גודל המדגם. כמו כן נניח כי השכיחות של מחלה זו באוכלוסיה הכללית היא 1%. שכיחות המחלה היא ההסתברות המקדימה הנדרשת על פי משפט בייס. בדיקת הסריקה מבוצעת ל-10,000 אנשים.

נמחיש את חישוב הסתברות גילויי השווא (מבלי להשתמש בפורמליזם של משפט בייס) באמצעות ציור 1.

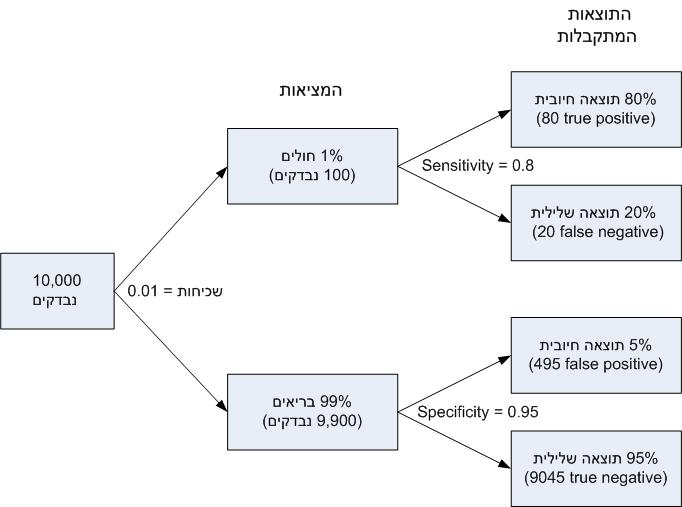
כדי לחשב איזה חלק של התוצאות החיוביות הן שגויות, עלינו להתחשב לא רק במיקרים של false positive הנקבע על ידי רמת המובהקות של הסריקה (הענף התחתון של הציור), אלא גם במקרים של true positive (הענף העליון של הציור). לכן, המספר הכולל של תוצאות חיוביות הוא
false positive + true positive = 495 + 80 = 575. מתוכן 495 הן false positive. לפיכך, ההסתברות לתוצאה שגויה היא 495/575 = 86%. תוצאה גרועה בצורה קיצונית, גדולה בהרבה מרמת המובהקות של 5% שבחרנו לניסוי.

ראוי לציין, כי כאשר השכיחות של המחלה הנבדקת גבוהה יותר, ההסתברות לתוצאה שגויה נמוכה יותר. למשל, עבור שכיחות מחלה של 10% מקבלים הסתברות תוצאה שגויה של 36%. גם תוצאה זו גבוהה בהרבה מרמת המובהקות של 5%.

להלכה, אבחון מוקדם של מחלה הוא דבר חיובי. למעשה, כאשר ההסתברות לאבחנה שגויה כה גבוהה כמו בדוגמה לעיל, הרי שמתעורר ספק רב בדבר אמינותן של בדיקות הסריקה למיניהן.

בעיית בדיקות המשמעות הסטטיסטית

בניסויים קליניים מקובלת רמת מובהקות של 5% כגודל המפריד בין תוצאה משמעותית סטטיסטית לבין תוצאה שאיננה משמעותית. המדד לבצוע ההבחנה הוא מיודעינו p-value.

נניח כי במהלך תקופה מסוימת חברת תרופות מבצעת ניסויים לבדיקה של 1,000 תרופות שונות לטיפול במחלה כלשהי. החוקרים בוחרים במדגם הנותן עוצמה (power) של 80% (זהו הערך המקובל בניסויים קליניים. כמובן עדיפה הייתה עוצמה של 90% ומעלה, אבל זה דורש מדגמים גדולים מאד ובדרך כלל בלתי ניתנים להשגה).

נניח כי ב-100 מתוך 1,000 ההתרופות (10%) מתקבלת התופעה המבוקשת (זוהי ההסתברות המקדימה הדרושה למשפט בייס). כמו כן נניח כי באחד הניסויים מתקבל
p-value = 0.047, ומאחר שהתקבל p-value ≤ α, החברה מצהירה כי נמצאה תרופה למחלה, ומפרסמת את תוצאות הניסוי בספרות המקצועית (ומוציאה פטנט, ומרוויחה הרבה כסף).

אבל מסתבר כי טענה זו תהיה שגויה לא ב-5% של המיקרים (רמת המובהקות), אלא ב-36%. כמו בבדיקות הסריקה, המספר הגבוה של שגיאות נובע מכך כי מספר שגיאות ה-false positive (כאשר אין תופעה) גדול  ממספר ה-true positive (כאשר יש תופעה).

נמחיש את החישוב בציור 2

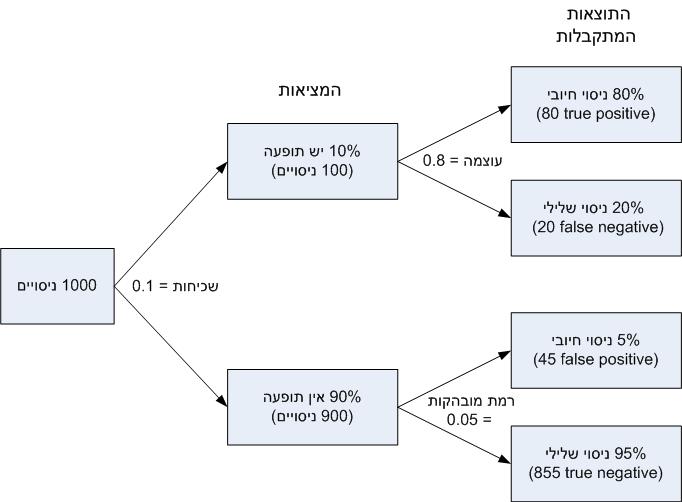
המספר הכולל של תוצאות חיוביות הוא
false positive + true positive = 45 + 80 = 125. מתוכן 45 הן false positive. לפיכך, ההסתברות לתוצאה שגויה היא 45/125 = 36%.

חסם תחתון להסתברות תוצאה שגויה

ברוב המיקרים ההסתברות המקדימה בניסויים קליניים איננה ידועה. ניתן לחשב את
p-value, אבל לא ניתן לחשב את הסתברות התוצאה השגויה על ידי משפט בייס.

למרות זאת זאת נוכל לחשב את החסם התחתון של הסתברות התוצאה השגויה אם נאמץ את ההנחה כי הסיכוי מלכתחילה לקבלת תופעה אמיתית (של ההתערבות הרפואית) אינו עולה על 50% (כי זה לא מתקבל על הדעת להניח הסתברות גבוהה יותר עוד בטרם התחיל הניסוי).

אם נחזור על החישובים שבוצעו לעיל תוך שימש בשכיחות של 50% (במקום 10%), נקבל הסתברות לתוצאה שגויה של 26%, עדיין גבוהה משמעותית מ-5%.

סכום

כאשר חוקר מבצע ניסוי בודד, מקבל p-value ≤ α, ומצהיר שקיבל תופעה אמיתית – הרי שטענה זו תהיה שגויה לפחות ב-26% מהמיקרים. לא פלא כי קיימת בעיה של שיחזור תוצאות בניסויים קליניים המבוססים על מבחני משמעות סטטיסטית.

מקורות

An investigation of the false discovery rate and the misinterpretation of
p-values
https://royalsocietypublishing.org/doi/full/10.1098/rsos.140216

The problem with p-values
https://aeon.co/essays/it-s-time-for-science-to-abandon-the-term-statistically-significant

The perils of p-values
http://chalkdustmagazine.com/features/the-perils-of-p-values/

§