חלק שני: משמעות סטטיסטית ומשמעות קלינית

מבוא

96% של הפרסומים בתחום הביו-רפואה מדווחים על תוצאות בעלות משמעות סטטיסטית ^[1] (statistical significance).

אבל משמעות סטטיסטית אינה אומרת דבר על המשמעות הקלינית (clinical significance) של התוצאה. יתכן מצב של תוצאה משמעותית סטטיסטית אך חסרת משמעות קלינית, או לחלופין, בעלת משמעות קלינית אך חסרת משמעות סטטיסטית.

נבחן את שני המושגים האלה.

משמעות סטטיסטית

Null hypothesis

תוצאות מחקר מדעי מבוססות בדרך כלל על ניסויים. ניסויים אלה הם מבחנים סטטיסטיים של השערות (hypothesis testing).

השערת האפס (null hypothesis), המסומנת H₀, מגדירה מהו ערכה של התופעה הנבדקת.

הערה: אני לא מכיר את השמות בעברית של כל המושגים המוזכרים כאן. התרגום, לטוב ולרע, הוא שלי.

במחקרים ביו-רפואיים מקובל כי ערכה של השערת האפס שווה לאפס – כלומר, אין הבדל בתופעה בין הקבוצות הנבדקות (בין קבוצת הטיפול החשופה להתערבות רפואית לבין קבוצת הבקרה שאינה חשופה להתערבות רפואית)

למשל, ניסוי הבודק האם התרופה rapamycin מאריכה את חייהם של עכברים. במקרה זה השערת האפס היא:
משך החיים של עכברים המקבלים את התרופה = משך החיים של עכברים שלא מקבלים את התרופה
במילים אחרות, התרופה לא מאריכה חיי עכברים. החוקר ינסה להוכיח את יעילות התרופה על ידי הפרכת השערת האפס.

Significance level

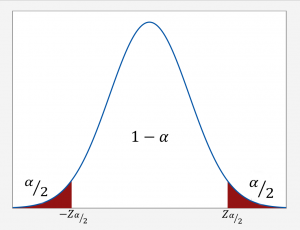
רמת המובהקות‏ (significance level), המסומנת באות α, היא מדד לעוצמה הדרושה של העדות לצורך דחיית השערת האפס. זוהי ההסתברות לגילוי של התופעה שאינה קיימת (false positive), ונקראת גם שגיאה מסוג 1 (type I error). החוקר קובע את רמת המובהקות שהוא דורש לפני ביצוע הניסוי.

רמת המובהקות היא ההסתברות לדחיית השערת האפס כאשר היא נכונה. לדוגמה, רמת מובהקות של 0.05 מציינת כי יש סיכון של 5% כי נסיק שיש הבדל בין הקבוצות הנבדקות, כאשר לאמיתו של דבר אין הבדל כזה. רמת מובהקות נמוכה יותר מציינת כי החוקר דורש עדות חזקה יותר לפני שהוא דוחה את השערת האפס.

Confidence level

המשלים של רמת המובהקות נקרא רמת סמך (confidence level), וערכה CL = 1 – α. כך שעבורCL = 95% ,α = 5%.  

Confidence interval

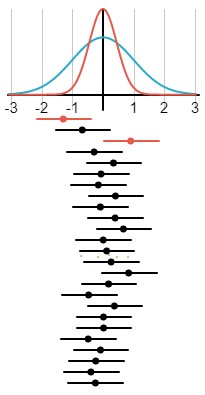
מרווח הבטחון (confidence interval) של מדגם סטטיסטי הוא תחום הערכים בתוכו נמצא (בהסתברות CL) הערך הממוצע של המדגם.

בגלל האופי האקראי של הנתונים, הרי שההסתברות כי שני מדגמים של אותה אוכלוסיה יתנו מרווח בטחון זהה היא נמוכה. אבל אם נחזור על הניסוי מספר רב של פעמים, אזי אחוז מסוים של מרווחי הבטחון יכיל את ממוצע האוכלוסיה. אחוז זה של מרווחי הבטחון הוא רמת הבטחון (CL) של המרווח.

P-value

להבדיל ממתמטיקה, אין הוכחות במדע. גודל סטטיסטי הנקרא p-value מכריע את גורלה של השערת האפס.

p-value היא ההסתברות לקבלת התופעה הנבדקת בניסוי, בהנחה שהשערת האפס נכונה.

p-value מנסה לענות על השאלה מהי ההסתברות שנדחה את השערת האפס כאשר למעשה היא נכונה. במילים אחרות, מהי ההסתברות שהתופעה אותה אנו חוקרים לא נגרמה על ידי ההתערבות הרפואית אלא על ידי רעש או יד המקרה.

אם p-value המתקבל בניסוי קטן מרמת המובהקות שנבחרה, p-value < α, אזי המסקנה היא שהשערת האפס איננה נכונה, ועלינו לדחותה.

אופן הצגת הנתונים במחקר ביו-רפואי

להלן דוגמה של הצורה המקובלת להצגת תוצאות ניסוי במחקר ביו-רפואי הבוחן למשל השפעה של מזון F על הסיכוי לחלות במחלה D.

1.17, 95% CI (1.05-1.34)

1.17 אומר כי אכילת F מגדילה את הסיכון היחסי לחלות במחלה D ב-17%.

95%CI אומר כי מדובר במרווח בטחון (CI) בעל רמת סמך (CL) של 95% (5% = α).

(1.05-1.34) הוא מרווח הבטחון CI (בתוכו בהסתברות CL נמצא ממוצע המדגם).

המשמעות של הביטוי לעיל היא כי אם יבוצעו עוד ניסויים כדוגמת זה שמדווח במחקר, אזי ב-95% מתוכם הסיכון היחסי הממוצע (1.17) ימצא בתוך תחום ה-CI של 1.05-1.34, ואילו ב-5% הוא ימצא מחוץ לתחום זה.

אם בהתערבות כלשהי הסיכון יחסי יורד, התוצאה תראה למשל כך:

0.85, 95% CI (0.74-0.96)

דוגמה של פרסום באתר המדעי BMJ

Higher coffee consumption is associated with lower risk of all cause and cause-specific mortality
https://ebm.bmj.com/content/21/3/108

משמעות קלינית

בעוד שמשמעות סטטיסטית מתייחסת לשאלה האם תופעה קיימת, הרי שמשמעות קלינית מתייחסת למדד הכמותי של גודל התופעה (effect size). שום מבחן סטטיסטי לא יכול לענות על השאלה האם התופעה שהתקבלה גדולה מספיק כדי להיות בעלת משמעות קלינית. כאן החוקר חייב להפעיל את שיקול הדעת המקצועי שלו בנשוא הניסוי.

מתי ניסוי הוא חסר משמעות סטטיסטית, אבל עשוי להיות בעל משמעות קלינית? למשל כאשר מספר המשתתפים היה קטן, אבל ההבדל בין הקבוצות הנבדקות היה גדול – כלומר גודל התופעה היה משמעותי.

התקבל p-value > α, והחוקר לא יכול לדחות את השערת האפס (וממילא הסיכוי שהמחקר שלו יתפרסם הוא קלוש). זהו מצב של כשלון בהפרכת השערת האפס, בעוד שתופעה אמיתית קיימת.

כדי להתמודד עם מצב כזה, נדרשת הגדלה של עוצמת המבחן הסטטיסטי (power).

Power

עוצמה של מבחן סטטיסטי היא ההסתברות שהניסוי יזהה תופעה אשר אכן קיימת (true positive). מתמטית power = 1 – β, כאשר β היא ההסתברות להחטאה של תופעה קיימת (false negative), ונקראת גם שגיאה מסוג 2 (type II error). כדי להקטין את ההסתברות להחטאה של תופעה קיימת, צריך להגדיל את עוצמת הניסוי.

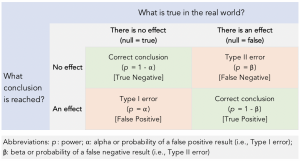
שלושה גורמים משפיעים על העוצמה הסטטיסטית של ניסוי:

• רמת המובהקות (α) אותה דורש החוקר
• גודל המדגם (N)
• β (שגיאה מסוג 2)

בניסויים קליניים מקובל לדרוש רמת מובהקות של 5% (רמת סמך 95%). לחוקר המתכנן ניסוי יש השפעה בעיקר על גודל המדגם, ממנו נגזרת העוצמה הסטטיסטית (ככל שהמדגם גדול יותר, העוצמה הסטטיסטית עולה, והסתברות ההחטאה יורדת). גודל התופעה מתברר רק בתום הניסוי.

סכום

ניסוי יכול להיות משמעותי סטטיסטית, בעל עוצמה ורמת סמך גבוהים, אך בעל משמעות קלינית חלשה ולא משמעותית.עם זאת, קיימים מיקרים של תוצאות חלשות סטטיסטית אשר מקנות תובנות חשובות להמשך המחקר.

מקורות

[1] https://www.ncbi.nlm.nih.gov/pubmed/26978209

 

---