קורונה – מודלים אפידמיולוגיים

הקדמה

מגיפת הקורונה העשירה את הסלנג שלנו בביטויים חדשים לרוב, ביניהם: בידוד עצמי, ריחוק חברתי, השטחת העקומה, איסטרטגיית יציאה, חזרה לשיגרה.

בימים הראשונים של המגיפה הסבירו לנו המומחים כי מטרת הריחוק החברתי היא לשטח את העקומה כדי למנוע את קריסת מערכת הבריאות.

במאמר זה נעשה הכרה בסיסית עם הכלים המתמטיים באמצעותם מחשבים את אותן עקומות – המודלים האפידמיולוגיים.

מודלים תאיים

מודלים תאיים (compartmental models) היא משפחה גדולה של מודלים מתמטיים בהם משתמשים האפידמיולוגים לחיזוי של התפשטות מחלות. במודל תאי האוכלוסיה מחולקת לתאים, כאשר מניחים כי כל הפרטים בתא נתון הם בעלי תכונות זהות. מודלים אלה מבוססים על תאוריה אשר פיתחו Kerman-McKendrick בתחילת שנות השלושים של המאה ה-20.

מודל SIR

קיימים מודלים אפידמיולוגיים רבים (SIR, SIS, SEIS, SEIR, SIRS). אנחנו נתמקד בפשוט מכולם – SIR. מודל SIR מורכב משלושה תאים:

• S – מספר הפגיעים להדבקות (Susceptible)
• I – מספר המודבקים (Infectious)
• R – מספר המבריאים (Recovered)

מודל SIR מתאר איך מספר האנשים בכל תא משתנה בתלות בזמן

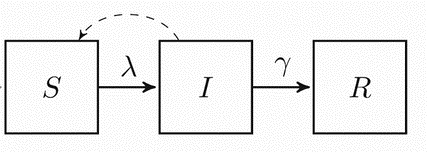
ציור 1 – מודל SIR

λ מגדיר את עוצמת ההדבקה של אוכלוסיה S כאשר היא באה במגע עם אוכלוסיה I. חשוב להדגיש כי קצב ההדבקות איננו קבוע, אלא תלוי במספר המודבקים (λ = λ(I, באופי המגע ובמישכו.

γ מגדיר את קצב ההחלמה של אוכלוסיית I.

החץ המקווקו מסמל את המגע בין אוכלוסיית תא I לבין אוכלוסיית תא S.

למען הפשטות נניח כי האוכלוסיה הכוללת N היא קבועה (dN/dt = 0) וכי המבריאים אינם פגיעים יותר למחלה (האם נכון עבור קורונה?), אזי,

עכשיו נוכל לרשום מערכת של שלוש משוואות דיפרנציאליות רגילות (ODE) המתארות את מודל SIR

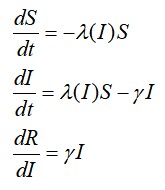
מספר ההתרבות הבסיסי R₀

מספר ההתרבות הבסיסי (R₀ (basic reproduction number הוא הפרמטר החשוב ביותר בניתוח כמותי של מודלים אפידמיולוגיים, והוא מוגדר כמספר הממוצע של מיקרים משניים באוכלוסיית הפגיעים להדבקות S, הנגרמים ממקרה בודד בתא I . קיימות שיטות רבות לחישוב גודל זה במודלים תאיים. נתבונן בחישוב פשוט עבור מודל SIR, המנסה לענות על השאלה מהם התנאים לדעיכתה של מגיפה.

נניח אוכלוסיה S בעלת N בני אדם. עוצמת ההדבקה λ נתונה על ידי הביטוי

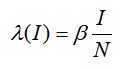
כאשר β הוא המכפלה של קצב המגעים בין מודבקים לשאינם מודבקים והסתברות ההדבקות בהנתן המגע, ואילו I/N הוא יחס המודבקים מתוך כלל האוכלוסיה. הצבה למערכת המשוואות נותנת

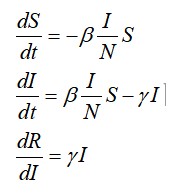
 נניח כי בזמן t = 0 יש חולה אחד. כלומר I(0) = 1, S(0) = N – 1.

המחלה לא תתפשט אם יתקיים

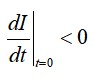
נציב את תנאי ההתחלה לביטוי ל-dI/dt ונקבל

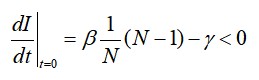
עבור N גדול בהרבה מאחד נקבל כי התנאי לדעיכת המחלה הוא

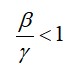
מספר ההתרבות הבסיסי מוגדר על ידי

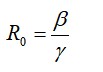
להזכירכם, β הוא המכפלה של קצב המגעים בין מודבקים לשאינם מודבקים והסתברות ההדבקות בהנתן המגע, ואילו γ הוא קצב ההחלמה של אוכלוסיית החולים I.

דוגמה של גרף SIR עבור N = 1000, β = 0.2, γ = 0.1, I(0) = 1 מוצגת במיור 2.

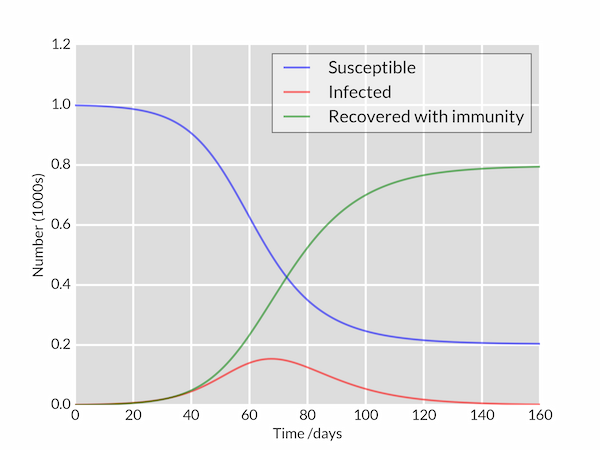
ציור 2 – גרף SIR

ערכים של R₀ עבור מחלות מדבקות שונות מוצגים בטבלה

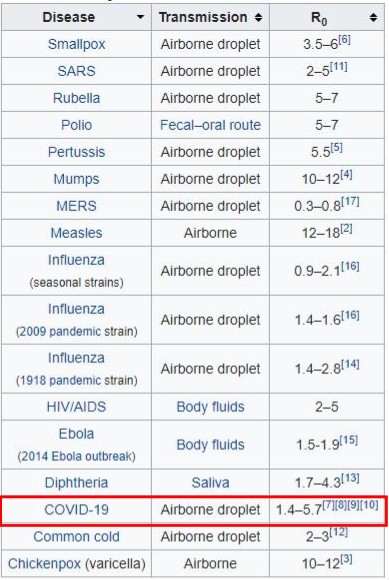
התחום של R₀ עבור COVID-19 הוא רחב מאד, ומכאן נובעת השונות הגדולה של ההערכות לגבי התמותה הצפויה מהמחלה, וצורתה של עקומת המודבקים I.

לסיום מצורפת סימולציה מעניינת של מגיפה באמצעות מודל SIR.